Nombre d'or ou "divine proportion"

Connu depuis la plus haute Antiquité de manière empirique, étudié par Pythagore au VIe siècle avant J.-C., le nombre d'or n'eut sa définition consignée par écrit que trois siècles plus tard par le mathématicien grec Euclide dans ses Éléments de géométrie.

Ce rapport harmonique particulier s'exprime par un nombre irrationnel qu'on désigna plus tard par la lettre 'phi' de l'alphabet grec (capitale Φ, minuscule φ ou ϕ) par allusion au sculpteur Phidias.

Le nombre d'or, bien qu'étant une grandeur purement arithmétique, est aussi une mystérieuse expression à laquelle on attribue certaines propriétés esthétiques.

Une explication scientifique stipule que le nombre d'or possède des propriétés troublantes : " Nous sommes mystérieusement accordés à ce nombre, car la section d'or agit sur nos sens et, par eux, sur notre cortex cérébral, essentiellement le droit, mais sans doute pas exclusivement, c'est pour cette raison que nous sommes inconsciemment enclins à trouver belles les grandeurs de tous ordres qui entrent dans cette relation. " (La Recherche 278 juillet-août 1995 volume 26)

Au milieu du XVe siècle, le nombre d'or est non seulement bien connu des mathématiciens mais son application par les artistes n'est pas rare. S'il fallut attendre la date de 1509 pour que soit publié, à Venise, un ouvrage qui lui soit entièrement consacré, le De divina proportione de Luca Pacioli, ami de Léonard de Vinci, il n'en était pas moins une donnée essentielle de la recherche de l'harmonie tant en architecture qu'en peinture.

Si l'on prend l'exemple d'un cercle de centre O dans lequel on trace les deux pentagones, l'un convexe et l'autre étoilé, de côté respectivement AB et AC : AC/AB = ?.

Le triangle ACD est le triangle dit fondamental, dans lequel CA/CD = ?.

Euclide, cependant, ne s'attache pas à donner une évaluation chiffrée de ce rapport. La valeur numérique de Φ n'a pu être évaluée par une méthode mathématique et rigoureuse que grâce à la trigonométrie au IIe siècle av. J.-C. Elle est en valeur approchée de 1,618.

L'expression arithmétique de ce rapport est le nombre 1,618. Appliqué à un rectangle de 5 cm sur 3 cm, nous avons : 5 cm : 1,618 = 3,09 cm et 3 cm : 1,618 = 1,85 cm ; il est possible de porter ces résultats sur notre rectangle de quatre manières différentes :

Il en résulte quatre "points d'or", parmi lesquels l'artiste peut choisir où placer l'élément le plus important de son œuvre, avec l'assurance de l'avoir situé à l'endroit le plus approprié, esthétiquement parlant. (Ex. Vélasquez "L'adoration des Mages", le visage de l'enfant Jésus à un "point d'or")

Les artistes utilisent le rapport entre 5 et 8, deux termes de la suite de Fibonacci. En fait, la valeur du rapport 5/8 se rapproche de la valeur du nombre d'or qui est 0,618

Le respect de cette proportion engendre des images dissymétriques mais beaucoup plus agréables à l'œil.

Lorsque nous regardons attentivement certains végétaux, on peut y découvrir le nombre d'or dans leur dynamique de croissance qui provoque l'apparition de ces spirales liées au nombre d'or. En effet, lors de la croissance de ces végétaux, on remarque la constance du nombre d'or. Par exemple dans la pomme de pin on retrouve 5 spirales dans le sens des aiguilles d'une montre et 8 dans le sens opposé, ou 8 et 13 chez l'ananas ou même 34 et 58 pour le tournesol (rappelons-nous, par exemple, que le rapport entre 5 et 8 s'approche grandement du nombre d'or...).

C'est surtout à propos du corps et du visage humain qu'est invoqué le nombre d'or. Par exemple le nombril divise le corps humain suivant le nombre d'or. En termes plus précis, on pourrait dire que le rapport de la hauteur totale du corps humain à la hauteur du nombril est égal au nombre d'or ! De plus, on dit que le rapport de la première phalange à la deuxième, ou de la deuxième à la troisième, est égal au nombre d'or.

 

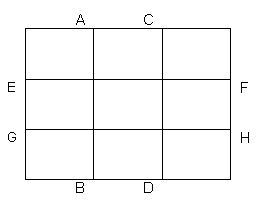
La règle des tiers

La division du rectangle selon la règle d'or permet de déterminer les " lignes de force " horizontales (AB et CD) et verticales (EF et GH).

Cela équivaut à diviser l'image horizontalement et verticalement en tiers.

L'intersection des "lignes de force" produit 4 points forts.